-
R 기초 통계 / 회귀 분석이란? (상관분석, 설명력, 다중공선성)머신러닝 with R 2019. 8. 22. 20:36
회귀분석이 쓰이는 이유?
- 가장 기본적인 분석으로 모형의 결과가 선형 1차 방정식으로 매우 단순하고 매우 잘 맞는다.
- 입력 변수의 회귀 계수를 이용해 각 변수들의 영향력을 쉽게 파악할 수 있어 매우 투명하다
- 데이터가 적더라도 모형을 만들 수 있으며 데이터가 많더라도 모형을 만드는데 시간이 오래 걸리지 않는다.
- 하지만 선형적이지 않는 데이터는 선형성을 가지도록 변수를 변환해야 한다.
상관분석
상관분석(correlation analysis)은 x값과 y 값, 두 변수 간의 상관관계를 탐색하기 위해 사용된다. 즉 연속적인 두 변수 간에 선형 관계가 있는지 탐색 및 확인하는 방법이다. 상관 분석에서 구해지는 상관 계수 r은 두 변수의 직선적인 연관성의 정도를 나타낸다.
간단히 말해서, x가 증가하면 y도 증가하는가? 혹은 감소하는 가?를 나타낼 수 있다. 쉽게 말해서 한 변수의 변화가 다른 변수의 변화에 영향을 미치는 가에 대한 관계를 분석하는 것이다.
예를 들어, 광고비가 늘어나면 매출액도 늘어나는가? GDP 가 높을수록 국민들의 행복도도 늘어나는 가? 를 생각해 볼 수 있다.
상관관계는 두 변수간의 관련성만을 의미할 뿐 인과관계를 밝히지 못한다.
(상관 계수 r은 선형적인 관계의 정도를 의미하는 것으로 통계학에서 Pearson 상관계수를 의미한다.)

회귀분석
회귀분석(regression anaylsis)의 기본은 상관분석에서 시작된 것으로 상관분석의 확장이라고 생각하면 좋다.
회귀분석은 입력 변수와 목표 변수 간의 인과관계를 파악하기 위해 사용된다.
상관 분석은 하나의 x변수와 y변수만의 관계를 평가할 수 있다면 회귀분석은 한 개 이상의 독립변수들(x)이 종속 변수(y)에 미치는 영향을 알 수 있다. 회귀분석을 이용하면 측정한 x 값으로 y 값을 추정할 수 있다.
회귀 방정식은 선형 방정식과 매우 유사하다.
선형 방정식 y = ax + bx
회귀 방정식 y = β0 + β1 x+ ε
회귀방정식 도출을 위한 핵심이라고 할 수 있는 '최소제곱법(Least-squares method)'는 오차(ε)의 제곱의 합이 최소가 되도록 회귀 계수를 구하는 것이다.
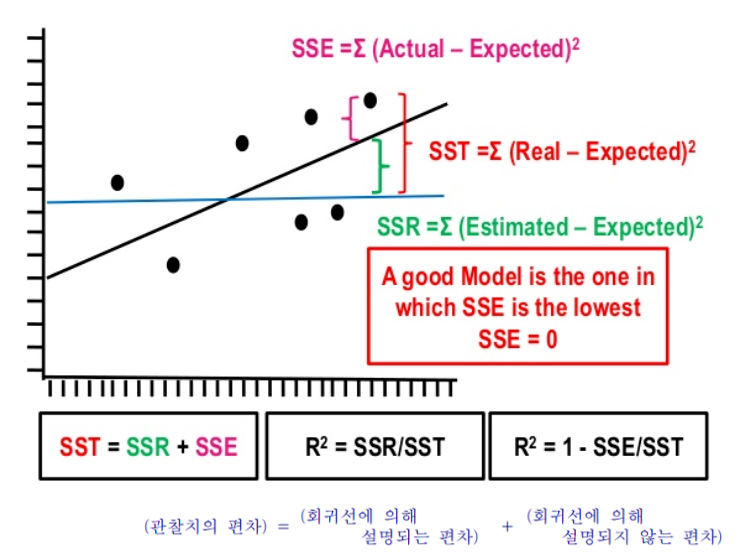
다음으로 회귀분석에서 결정계수(설명력)는 무엇일까?
결정계수는 표본으로 추정된 회귀선이 관찰치를 얼마나 적절히 설명하는 가를 나타내는 척도이다.
R^ = SSR/SST = 1 - SSE/SST
- 추정된 회귀선에 모든 관찰치가 놓이면 SSE = 0 이기 때문에 R^2 = 1이 된다.
- 결정계수 R^2 = 상관계수 r^2
- 결정계수 값이 1에 가까울수록 추정된 회귀선은 유의하지만, 0에 가까울수록 의미가 없게 된다.
- 기울기가 0이면 R^2 도 0이다.
다중회귀 분석
다중 회귀 분석은 단순 회귀 분석의 확장판으로 입력 변수가 2개 이상일 때의 분석이다.
다중회귀 분석: y = β0 + β1 x+ β2x2 +... +βpxp + ε
각각의 입력 변수 x가 목표 변수를 설명하는 크기는 회귀계수 β1, β2, ..., βp로 비교할 수 있다.
입력 변수 x 가 많아질수록 설명력이 올라가는 장점이 있지만, 각 변수들의 영향력을 고려해야 한다.
영향력이 거의 없는 입력 변수가 있을 수 있으므로 영향력이 큰 변수만을 추출해야 하는 '변수 선택'의 과정이 요구된다.
또한 '다중공선성' 이라 불리는 문제가 발생할 수 있는데, 입력 변수 간들의 관계가 독립적이지 않을 수 있다는 의미이다.
이렇게 입력 변수 간 다중 공선 성이 존재할 때의 문제는?
- 회귀 계수의 분산이 커져 오차가 커지고, 따라서 예측 정확도가 떨어진다.
- 모델을 평가하는 결정계수(R^2)의 값이 실제보다 크게 나올 수 있다. 즉, 모형의 평가를 신뢰할 수 없다.
- over-fitting 문제가 발생할 수 있다.
진단 방법은?
- 특정 변수의 상관계수가 매우 클 때
- 입력 변수 하나가 들어가거나 빠질 때 회귀계수의 크기가 크게 변할 때
- 회귀 계수의 부호가 상관분석과 반대로 나타날 때
- 중요한 입력 변수가 유의하지 않게 나올 때
- VIF(분산 팽창 요인) 값이 10 이상일 때
이러한 경우에는 다중공선성 문제를 의심해 볼 수 있다.
회귀분석에서 변수 선택의 방법
1) 입력(Enter) : 모든 가능한 변수들의 조합을 회귀분석 해 보는 방법
2) 전진 선택법(Forwards): 가장 중요하다고 생각되는 변수부터 하나씩 골라가며 넣는 방법이다. 더 이상 중요한 변수가 없다고 생각될 때 중단하여 준다. 한번 넣은 변수는 다시 뺄 수 없다.
3) 후진 제거법(Backwards): 모든 변수를 포함시켜 규모가 큰 회귀 방정식으로부터 출발하여 중요하지 않다고 생각되는 변수를 하나씩 제거하는 것이다. 더 이상 제거시킬 변수가 없을 때 중단한다. 한번 뺀 변수는 다시 넣을 수 없다.
4) 단계 선택법(Stepwise): 전진 선택법과 비슷하게 중요한 변수를 하나씩 추가 선택해 가는데 미리 들어간 변수와 새로운 변수를 검토해보면서 추가와 제거를 할 수 있다.
회귀분석의 기본 가정
1) 선형성: 입력 변수(x)와 목표 변수(y) 사이에 선형적인 관계를 의미한다. 산점도를 이용해 선형성을 파악할 수 있으며, 만약 다른 형식일 경우 입력 변수를 변환하여 선형적인 관계로 만들어야 한다.
2) 등분산성: 오류항은 정규분포를 따르며 일정한 분산을 갖는다. 즉, 오류 항의 분산은 상이한 입력값이 들어오더라도 일정해야 하며, 가정이 위배될 경우 추정이 편향된다.
3) 비공선성(입력 변수 간의 독립성): 입력 변수 사이에 상관관계 (선형성)가 있으면 안 된다. 이럴 경우 추정 값이 편향될 수 있다.
4) 이상치가 없어야 함: 이상치는 모형을 심하게 왜곡시킬 수 있어 모형 생성 전에 제거해야 한다.
회귀분석이 기본 가정을 만족시키는지는 다음과 같은 진단 도표를 통해 확인할 수 있다.

plot()을 통해 생성된 진단도표 1) Residuals VS. Fitted :
x축 = 선형 회귀로 예측된 y값, y축 = 잔차를 보여 준다.
선형 회귀에서 오차는 평균이 0이고, 분산이 일정한 정규분포를 가정하였기 때문에 예측된 y 값과 무관하게 잔차의 평균이 0이고 분산은 일정해야 한다. 따라서 이 그래프에서는 기울기 0인 직선이 관측되는 것이 이상적이다.
즉, 점들이 빨간 선에 최대한 가까워야 이상적이라고 할 수 있다.
2) Scale-Location:
x축 = 선형 회귀로 예측된 y값, y축 = 표준화된 잔차를 보여준다.
이 경우에도 기울기가 0인 직선이 이상적이다. 만약 특정 위치에서 0에서 멀리 떨어진 값이 관찰된다면, 해당 점에 대해 표준화 잔차가 크다는 것이다.
즉, 회귀 직선이 해당 y를 잘 적합하지 못한다는 의미이다. 이런 점들은 이상치일 가능성이 있다.
3) Normal Q-Q: 점선은 정규 곡선을 의미한다. 잔차의 분포가 정규분포에 가까운지 보여주는데, 데이터가 완벽히 정규분포를 따른다면 점들이 모두 점선 위에 있어야 한다.
위 그래프는 점선 위에 대부분의 점들이 위치해 있기 때문에 정규성을 따른다고 볼 수 있다.
4) Residuals VS. Leverage:
x축 = 레버리지, y축 = 표준화 잔차를 보여준다.
레버리지는 설명 변수가 얼마나 극단에 치우쳐 있는지를 뜻한다. 예를 들어, 다른 데이터의 x값은 모두 1~10 사이의 값인데 특정 데이터만 9999라면 해당 데이터의 레버리지는 크다고 할 수 있다.
이런 데이터는 입력이 잘못되었거나, 해당 범위의 설명 변수 값을 가지는 데이터를 보충해야 하는 작업 등이 필요하기 때문에 유심히 살펴보아야 한다.
회귀모델의 평가
1) 전체 모형의 유의성:
전체 모형이 유의한지는 p-value가 0.05 미만인지를 통해 알 수 있다. 0.05 미만이라면 모델이 유의한 것이다.
2) 회귀 모형의 결정계수(R^2):
1에 가까울수록 유의하다.
3) 회귀식에서 유의한 변수 (끝에 별이 달린 것)과 회귀 계수(estimate)의 부호 및 크기
를 통해 평가할 수 있다.
반응형'머신러닝 with R' 카테고리의 다른 글
R과 기초통계 - 좋은 회귀 모형? 회귀분석의 확장 LASSO (0) 2019.08.24 R 기초 통계/ 로지스틱 회귀 분석 (Logistic Regression)이란? (0) 2019.08.23 R 머신러닝 지도학습의 모형 성능 평가 (0) 2019.08.07 앙상블(Ensemble) 모형 / Bagging과 boosting (0) 2019.07.28 R로 그래프 만들기 /ggplot2 패키지 /R 시각화 (0) 2019.07.25